#7
(a)
To find values of the function h at different x values, we go straight to that x value and find the corresponding y value of the graph.
From the graph, we have:
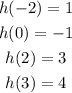
(b)
The domain of a function is the set of x-values for which the graph of the function is defined.
The range of a function is the set of y-values for which the graph of the function is defined.
Looking at the graph, we see that from
x = - 3 to x = 4, the function is defined.
Also, from
y = - 1 to y = 4, the function is defined.
Thus, we can write the domain and range as >>>>>
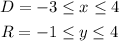
(c)
h(x) = 3 means y = 3
We will draw a horizontal line at y = 3 and see the points at which that line and curve crosses. Then, we will draw a perpendicular from that point to the x-axis. These are the values of x for which y = 3.
The graph:
We see from the graph drawn that for x = - 3, x = 2, and x = 4, the value of the function h is 3.
So,
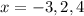
(d)
The values of x for which the function is ≤ 3 can be found by again drawing a line y = 3 and finding the places where the graph is BELOW that line.
Graph:
So, we can see that from x = - 3 to x = 2, the function is less than or equal to 3.
Thus,
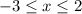
(e)
From x = - 3 to x = 3, the function changes several values. But the net change can be found by finding the respective values of the function at x = - 3 and at x = 3 and finding the difference.
At x = - 3, the function has a value of "3".
At x = 3, the function has a value of "4".
Thus, the net change is 4 - 3 = 1
Net Change = 1