Question

Find tan A and tan B for the following triangles. Enter answers as fractions in simplest form not decimals.

Answer 1

First, we must find the dimension of the missing side, for this, we use the Pythagoras theorem

`c^2=a^2+b^2`

Now, we replace these values an solve

`\begin{gathered} (3\sqrt[]{3})^2=a^2+3^2 \\ a^2=(3\sqrt[]{3})^2-3^2 \\ a^2=(9\cdot3)-9 \\ a^2=27-9 \\ a^2=18 \\ a=\sqrt[]{18}=\sqrt[]{9\cdot2}=3\sqrt[]{2} \end{gathered}`

The magnitude of the missing side is

`a=3\sqrt[]{2}`

Second, since we have all the sides defined we use the trigonometric tangent identity.

`\tan (x)=(O)/(A)`

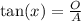
Where O is opposite and A is adjacent, now we can find tan A and B

Tan A

`\tan (A)=\frac{3}{3\sqrt[]{3}}`

Tan B

`\begin{gathered} \tan (B)=\frac{3\sqrt[]{2}}{3\sqrt[]{3}} \\ \tan (B)=\frac{\sqrt[]{2}}{\sqrt[]{3}} \end{gathered}`