Question

What order pair is in the solution set of 3x - 2y ≥ -1

Answer 1

The coordinates of the line are the solution of the given line and if they staisfy the given equation so, they are the solution of the equation : 3x - 2y ≥ -1​

A) (-2, -2.5)

Given equation :

`\begin{gathered} 3x-2y\ge-1 \\ 3(-2)-2(-2.5)\ge-1 \\ -6+5\ge-1 \\ -1\ge-1 \\ \text{Equation satisfy: So, (-2,-2.5) is the solution of }3x-2y\ge-1 \end{gathered}`

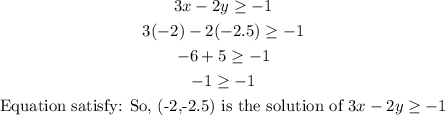
B) (2,4)

Given equation:

`\begin{gathered} 3x-2y\ge-1 \\ 3(2)-2(4)\ge-1 \\ 6-8\ge-1 \\ -2\ge-1 \\ \text{Equation does not satisfy: So, (2,4 ) is not the solution of }3x-2y\ge-1 \end{gathered}`

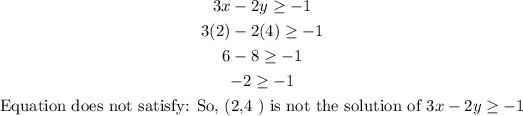
C) (1, 2.5)

Given equation:

`\begin{gathered} 3x-2y\ge-1 \\ 3(1)-2(2.5)\ge-1 \\ 3-5\ge-1 \\ -2\ge-1 \\ \text{Equationdoes not satisfy: So, (1, 2.5) is not the solution of }3x-2y\ge-1 \end{gathered}`

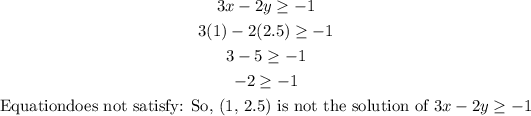
D) (-1,1)

Given equation:

`\begin{gathered} 3x-2y\ge-1 \\ 3(-1)-2(1)\ge-1 \\ -3-2\ge-1 \\ -5\ge-1 \\ \text{Equation doesnot satisfy: So, (-1,1) is not the solution of }3x-2y\ge-1 \end{gathered}`

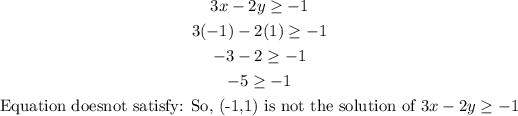
Answer: A) (-2, -2.5)