The given value is:
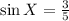
It is required to find the value of sec X given that X is an acute angle.
Recall the trigonometry identity:
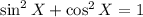
Substitute sin X=3/5 into the equation:

Since X is acute, the cosine of X must be positive.
It follows that:
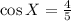
Recall the reciprocal identity:

Substitute cos X = 4/5 into the reciprocal identity:
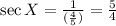
Hence, the answer is sec X = 5/4.
The answer is sec X = 5/4.