In this case, we'll have to carry out several steps to find the solution.
Step 01:
Data:
length of the shorter leg = ?
length of the longer leg = ?
length of the hypotenuse = ?
Step 02:
We must analyze the problem to find the solution.
x = length of the shorter leg
y = length of the longer leg
z = length of the hypotenuse
System of equations:
x = y - 7 (eq.1)
z = y + 7 (eq.2)
z² = x² + y² (eq.3)
eq.2 in eq.3
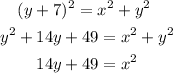
14y + 49 = x²
y - 7 = x * (-14) (eq.1)
14y + 49 = x²
-14y + 98 = -14x (eq.1)
__________________
147 = x² - 14x
x² - 14x - 147 = 0
Step 03:
Quadratic equation:
x² - 14x - 147 = 0
![x=\frac{-(-14)\pm\sqrt[]{(-14)^2-4\cdot1\cdot(-147)}}{2.1}](https://img.qammunity.org/2023/formulas/mathematics/college/gjrtfukgmha1zg4q1j22l79mlp8w0llf2x.png)
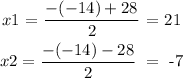
x = 21 (positive solution)
x = y - 7
21 + 7 = y
28 = y
z = y + 7 = 28 + 7 = 35
The answer is:
length of the shorter leg = 21
length of the longer leg = 28
length of the hypotenuse = 35