Answer:
The angles of ABC from smallest to largest: 52.83°, 57.53°, 69.64°
Step-by-step explanation:
Given:
AC = 18in, AB = 20 in, BC = 17 in
To find:
the angles of ABC from smallest to largest
To determine the angles, we will apply cosine rules:
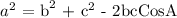

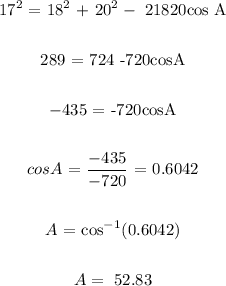


The angles of ABC from smallest to largest: 52.83°, 57.53°, 69.64°