We are given the function f(x) = x^3 - 6x^2 + 10x - 3, where x is a real number. We are supposed to translate it by (-2, 3) which means that we are moving the entore graph 2 units to the right and 3 units up.
The first thing to do is write the cubic function in the form f(x) = a(x - h)^3 + k where h is the horizontal translation and k is the vertical translation.
So, f(x) = x^3 - 6x^2 + 10x - 3 moved 2 units to the right and 3 units up would be written as:
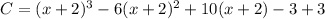
We can simplify this as:
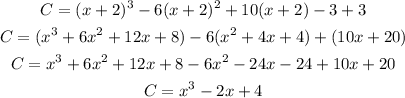
The graph crosses the y-axis when x = 0.
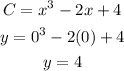
The point where the graph crosses the y-axis is (0, 4).