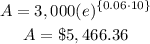if 3000 dollars is invested in a bank account at an interest rate of 6 percent per year find the amount in the bank after 10 years if interest is compounded quarterly
we know that
The compound interest formula is equal to
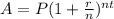
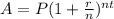
where
A is the Final Investment Value
P is the Principal amount of money to be invested
r is the rate of interest in decimal
t is Number of Time Periods
n is the number of times interest is compounded per year
in this problem we have
P=3,000
r=6%=6/100=0.06
t=10 years
n=4
substtute in the formula above
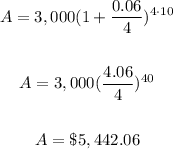
Part 2
compounded monthly
we have
P=3,000
r=6%=6/100=0.06
t=10 years
n=12
substtute in the formula above
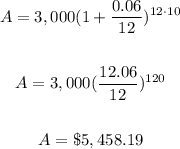
Part 3
continuously
we know that
The formula to calculate continuously compounded interest is equal to
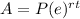
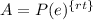
where
A is the Final Investment Value
P is the Principal amount of money to be invested
r is the rate of interest in decimal
t is Number of Time Periods
e is the mathematical constant number
we have
P=3,000
r=6%=6/100=0.06
t=10 years
substitute