Given,
The initial height of the ball, h₁=6 ft
The initial velocity of the ball, u=64 ft/s
The acceleration due to gravity, g=-32 ft/s²
The velocity of the ball when it reaches the maximum height will be, v=0 ft/s
From the equation of motion,
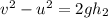
Where h₂ is the height covered by the ball to reach the maximum height.
On substituting the known values,

Thus the maximum height reached by the ball is
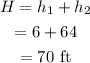
Thus the maximum height reached by the ball is 70 ft