Question

What Is the inequality and final answer to the problem

Answer 1

We know that

• The total money to spend is $20.

,

• The ride costs $5 plus $2.50 per kilometer.

,

• Let's call ,d ,the distance in kilometers.

Based on the given information, we write the following inequality.

`5+2.50d\leq20`

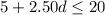
Notice that $5 is an independent term since it's a fixed cost. Then, we wrote 2.50 as the coefficient of the variable d since that's the ratio of dollars per kilometers. Additionally, the inequality sign is less than or equal to since we have a restriction of $20 maximum.

Now, we solve the expression for d.

`\begin{gathered} 2.50d\leq20-5 \\ 2.50d\leq15 \\ d\leq(15)/(2.50) \\ d\leq6 \end{gathered}`

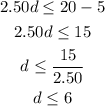
Therefore, the maximum distance you can ride for $20 is 6 kilometers.