Question

Consider the sequence: 0, 5, 10, 15, … Find A45

Answer 1

The given sequence:

`0,\text{ 5, 10, 15,}\ldots`

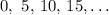
The first step is to identify what type of sequence this is.

We can observe that the terms differ by 5. Hence, the sequence is an arithmetic progression

Next, let us define the formula

The nth term of an arithmetic progression is:

`\begin{gathered} A_n\text{ = a + (n -1)d} \\ \text{Where a is the first term} \\ d\text{ is the co}mmon\text{ difference} \\ \text{ } \end{gathered}`

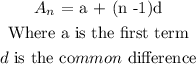
Next, we use the nth term to find the required term( 45th term)

We have:

a = 0, d = 5, n = 45

`\begin{gathered} A_(45)\text{ = 0 + (45-1)}*5 \\ =\text{ 44 }*\text{ 5} \\ =\text{ 220} \end{gathered}`

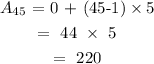
Answer: 220