Question

The scatter plot shows the average monthly temperature, x, and the monthly heating cost of a family, y, for 25 different months

Answer 1

Answer:

a) the predicted heating cost is $66.85

b) the predicted heating cost is $97.10

c) for an increase of 1 °F, the predicted decrease in heating cost is $1.21

Step-by-step explanation:

Given:

A scatter plot that shows the average monthly temperature, x, and the monthly heating cost of a family, y, for 25 different months

`\begin{gathered} the\text{ line of best fit is given as:} \\ y\text{ = -1.21x + 97.10} \end{gathered}`

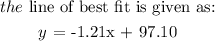
To find:

a) the predicted heating when the average temperature is 25 °F

b) the predicted heating when the average temperature is 0°F

c) the predicted decrease in monthly heating cost for an increase in 1°F

a) We will substitute x with 25 °F to get the predicted heating

`\begin{gathered} y\text{ = -1.21\lparen25\rparen + 97.10} \\ y\text{ = \$66.85} \end{gathered}`

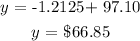
b) To get the predicted heating, we will substitute x with 0 °F

`\begin{gathered} y\text{ = -1.21\lparen0\rparen+ 97.10} \\ y\text{ = 0 + 97.10} \\ y\text{ = \$97.10} \end{gathered}`

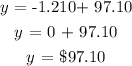
c) To get the decrease per monthly heating cost, we will find the predicted heating cost between two consecutive values of x

let x = 0, 1

when x = 0, y = $97.10

when x = 1 (this is an increase of 1 °F from the previous temperature)

y = -1.21(1) + 97.1

y = 95.89

The difference in heating cos when there is an increase of 1 °F:

difference = 95.89 - 97.10

difference = -1.21

Hence, for an increase of 1 °F, the predicted decrease in heating cost is $1.21