The triangle described is shown below (this is not the correct triangle but we need something to help):
To find the lenght of side AC we need to use the law os cosines:
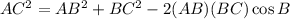
In this case we have:
![\begin{gathered} AC^2=12^2+18^2-2(12)(18)\cos 75 \\ AC^2=356.19 \\ AC=\sqrt[]{356.19} \\ AC=18.9 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7uyb3sxh4opwiacqbe2xh483mw8sf3toit.png)
Now, to find angle A can use the law of sines:
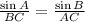
Then:

Therefore the correct answer is A.