Question

Find the minimum value of Z = x + 2y and subject to the constraints 2x + y ≤ 3, x + 2y ≤ 6, and x, y ≥ 0.

Answer 1

First, let's draw all the constrains in the coordinate plane to find the solution area:

The solution region is the orange area.

The minimum value of Z would happen for the minimum values of x and y (since both of them have positive coefficients), which are 0, so we have:

`\begin{gathered} Z=x+2y \\ x=0,y=0\colon \\ Z=0+2\cdot0 \\ Z=0 \end{gathered}`

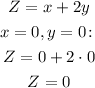
So the minimum value of Z is 0.