The formula for compound interest is:

Given data:
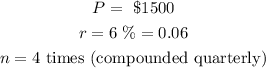
a. After ten years, that is t = 10 years, the amount in the account will be
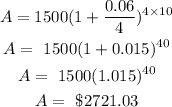
b. After twenty years, that is t = 20 years, the amount in the account will be:
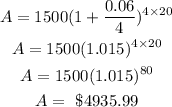
c. The time it takes for Harry's initial account value to double will be:

Therefore, the time it takes Harry's initial account to double is approximately 11 years