Question

Dale plans to build a balcony similar to the figure. Find the area and perimeter of the balcony. Round to the nearest whole unit. (Dimensions are in feet.)

Answer 1

The balcony is composed by a semicircle with radius r=5 units and a right triangle with a leg equal to 8 units.

Then, in order to find the perimeter, we need to find the missing leg of the triangle and the semi-circunference of the semicircle. So, let's draw a picture of our triangle:

We can find the missing leg by means of Pythagorean theorem, because,

`x^2+8^2=10^2`

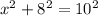
which gives

`x^2+64=100`

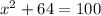
Then, by subtracting 64 to both sides, we have

`x^2=36`

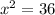
and by applying square root to both sides, we obtain

`\begin{gathered} x=\sqrt[]{36} \\ x=6 \end{gathered}`

Now, let's find the semicircunference. For a complete circle, the circunference formula is given by

`C=2\pi\cdot r`

where r denotes the radius. Then, the semicircunference is half this value, then, in our case, we have

`c=(C)/(2)=\pi\cdot r`

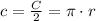
Then, the semicircunference is

`\begin{gathered} c=3.1416*5 \\ c=15.708 \end{gathered}`

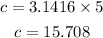
Then, the perimeter of the balcony is the sum of the 2 legs of the triangle plus the semi-circunference, that is,

`\begin{gathered} P=6+8+15.708 \\ P=29.708 \end{gathered}`

Therefore, by rounding to the nearest whole number, the perimeter is: 30 feet.

On the other hand, the area of the balcony is equal to the area of the triangle plus the area of the semicircle. Then, the area of the triangle is given by

`\begin{gathered} A_{\text{triangle}}=\text{base}* height \\ A_{\text{triangle}}=8*6 \\ A_{\text{triangle}}=48ft^2 \end{gathered}`

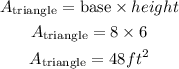
and the area of the semicircle is half the area of the complete circle, so we have

`\begin{gathered} A_{\text{semicircle}}=(\pi\cdot r^2)/(2) \\ A_{\text{semicircle}}=(3.1416*5^2)/(2) \\ A_{\text{semicircle}}=39.27ft^2 \end{gathered}`

Therefore, the area of the balcony is given by

`\begin{gathered} A=A_{\text{triangle}}+A_{\text{semicircle}} \\ A=48+39.27 \\ A=87.27ft^2 \end{gathered}`

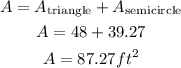
Hence, by rounding to the nearest whole number, the area of the balcony is: 87 square feet