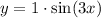Question

Type the equation for the graphbelow.HelpMTEMNy = [? ] sin([ ]x)Enter

Answer 1

Ok what we have here is a senoidal function, this type of functions have a general form:

`y=a\cdot\sin (b\cdot x)`

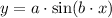
Where a is called amplitud and b is known as frecuency or angular frecuency. The amplitude indicates the value of the maximums and the minimums of the function. In this excercise if you look carefully you can see that the maximum value of the function (the highest point in the graph) is 1 and the minimum (the lowest point) is -1. This means that here a=1.

For now we have that:

`y=1\cdot\sin (b\cdot x)`

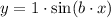
Now we need to find b. This one is a little more difficult.

First you must know about the concept of period. The period of a function like sine is given by the distance between two consecutive maximums or two consecutive minimums. This distance can also be calculated using the function zeroes (points where the graph intercepts the x-axis) like this:

In the case of this image the period is 2*pi, if we look at this distance in our graph you'll see that the period of our function is:

`(2)/(3)\pi`

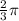
And the period is related to the frecuency b (the value we needed to find in the first place) by:

`\text{period}=(2\pi)/(b)`

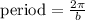
So:

`(2)/(3)\pi=(2\pi)/(b)`

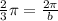
Using this we can find b:

`\begin{gathered} (2)/(3)\pi=(2\pi)/(b) \\ (2)/(3)\cdot(\pi)/(\pi)=(2)/(3)=(2)/(b) \\ (1)/(3)\cdot(2)/(2)=(1)/(3)=(1)/(b) \\ b=3 \end{gathered}`

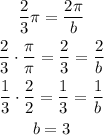
So the equation of our function is:

`y=1\cdot\sin (3x)`