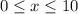Part A.
We are asked to find the y-intercept of the function. The y-intercept of a function is the value of y when the value of x is 0.
In this case, the y-intercept is given in the table:
When x is equal to 0, y is equal to 8. So the y-intercept is 8.
What this tells us about the horse is that he started his displacement when he was already 8 feet away from the barn.
Part B.
In this part, we need to find the average rate of change between x=1 and x=3. First, we label these limits as follows:
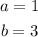
And now, we will use the average rate of change formula:
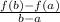
In this case since a=1 and b=3:
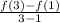
f(3) is the value of the function (the value of y) when x is equal to 3. And from the table, we can see that it is 158:
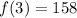
And we do the same for f(1), it is the value of y when x is equal to 1. And from the table, we see that it is 58:
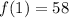
Going back and substituting these values into the average rate of change formulá:
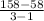
Solving these operations:
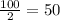
The average rate of change is 50 feet/hour. This average rate of change represents the number of feet that the horse moves in 1 hour. It is the displacement of the horse per hour.
Part C.
We are asked to find the domain of the function if the horse continued to walk at this rate until it traveled 508 feet.
To solve this problem, we can use an equation for the relationship between hours and distance:
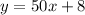
From the table, we have that x are the hours and y is the distance. That is because the distance is the multiplication of the rate of change by the hours, and since the horse started at 8 feet, we need to add that to the function.
With this function we find the value of x (the hours) when the distance traveled is 508 feet:
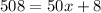
Solving for x:
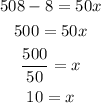
At 508 feet the horse has traveled for 10 hours.
Finally, to solve this part C of the problem we need the domain.
The domain is defined as the values possible for x. In this case, those values go from 0 hours to 10 hours (as we just found 10 hours is the limit)
So, the domain is:

Or you can also write as: