Question

8. Nate wrote the polynomial shown below on the board. Which value(s) of "n" would make the polynomial factorable? 16x2 - I. q 9 II. -9 III. 25 a. I only b. I and III only w c. I and II only d. I, II and III

Answer 1

By definition, a Perfect square trinomial has the following form:

`a^2\pm2ab+b^2`

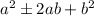
Perfect square trinomials can be expressed in Squared-binomial form, as following:

`(a\pm b)^2`

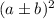
In this case, you know that the first term of the Perfect square trinomial Tia wrote on the board, is:

`4x^2`

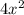
And the last term is:

`25`

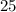
Then you can identify that:

`a^2=4x^2`

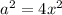
Solving for "a", you get:

`\begin{gathered} a=\sqrt[]{4x^2} \\ a=2x \end{gathered}`

Notice that:

`b^2=25`

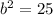
Solving for "b", you get:

`\begin{gathered} b=\sqrt[]{25} \\ b=5 \end{gathered}`

Knowing "a" and "b", you can write the following Squared-binomial:

`(2x+5)^2`

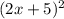
And determine that the missing term is:

`2ab=2(2x)(5)=20x`

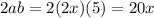
Therefore, the missing value is not a Perfect square, because it is not obtained by multiplying two equal Integers.

The answer is: Option B.