From the question
The slope of the graph is

using the equation of a line
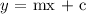
we can find the intercept C, where m is the slope of the line
From the question,
the height of the candle after 17 hours is 16.5 centimeters implies
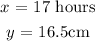
Using this information we can get the intercept C.
Substitute the values of x, y and m into the equation of line
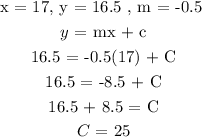
Now we need to find the height of the candle after 13hours
therefore, x = 13, m = -0.5, C = 25
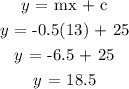
Therefore,
The height of the candle after 13hours is 18.5 centimeters