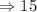Question

There are 19 animals on the farm which contains hens and goats. There are 68 legs in total. How many goats are there on the farm?151085

Answer 1

Step-by-step explanation:

Let the number of hens be

`=x`

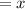
Let the number of goats be

`=y`

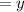
The number of animals on the farm is

`=19`

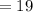
This can be represented in an equation below as

`x+y=19-----(1)`

The number of legs given in the question is

`=68`

Hens have 2 legs

Goats have 4 legs

So the number of legs can be represented in the equation below as

`2x+4y=68-----(2)`

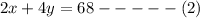
Step 1:

We will solve equations (1) and (2) simultaneously

`\begin{gathered} x+y=19----(1) \\ 2x+4y=68----(2) \end{gathered}`

From equation (1), we will make x the subject of the formula

`\begin{gathered} x+y=19 \\ x=19-y-----(3) \end{gathered}`

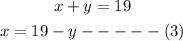
Step 2:

Substitute equation (3) in equation (2)

`\begin{gathered} 2x+4y=68 \\ 2(19-y)+4y=68 \\ 38-2y+4y=68 \\ 38+2y=68 \\ collect\text{ similar terms, we will have} \\ 2y=68-38 \\ 2y=30 \\ divide\text{ both sides by 2} \\ (2y)/(2)=(30)/(2) \\ y=15 \end{gathered}`

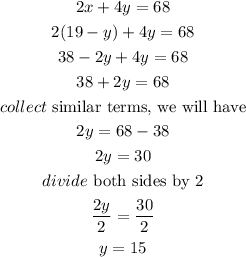
Hence,

The number of goats on the farm is

`\Rightarrow15`