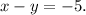Question

Use slope-intercept form to write an equation of a line passing through the given point and having the given slope. Express the answer in standard form.P(−4, 1); m = 1

Answer 1

Recall that the slope-intercept form of the equation of a line is as follows:

`\begin{gathered} y=mx+b, \\ where\text{ m is the slope of the line and \lparen0,b\rparen is the y-intercept.} \end{gathered}`

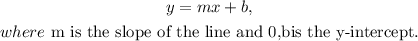
Also, the standard form of the equation of a line is as follows:

`\begin{gathered} Ax+By=C, \\ Where\text{ A, B, and C are integers and A>0.} \end{gathered}`

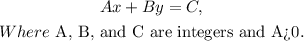
Then the slope-intercept form of an equation with slope m=1 is as follows:

`y=x+b.`

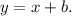
Now, we know that the line passes through (-4,1), then:

`1=-4+b.`

Adding 4 to the above equation we get:

`\begin{gathered} 1+4=-4+b+4, \\ 5=b. \end{gathered}`

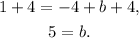
Therefore the slope-intercept form of the equation that passes through (-4,1) and has a slope of m=1 is:

`y=x+5.`

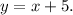
Adding -y-5 to the above equation we get:

`\begin{gathered} y-y-5=x+5-y-5, \\ -5=x-y. \end{gathered}`

Answer:

`x-y=-5.`