Question

You can smell perfume very shortly after opening the bottle. To show that it is not reaching your nose by diffusion, calculate the average distance (in m) a perfume molecule moves in one second in air, given its diffusion constant D to be 1.71 ✕ 10−6 m2/s.

Answer 1

Given:

Diffusion constant = 1.71 x 10⁻⁶ m²/s.

Let's find the average distance a perfume molecule moves in air.

Apply the formula:

`x_(rms)=√(2Dt)`

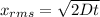
Where:

D is the diffusion constant

t is the time = 1 second.

Thus, we have:

`\begin{gathered} x_(rms)=\sqrt{2*1.71*10^(-6)*1.00} \\ \\ x_(rms)=\sqrt{3.42*10^(-6)} \\ \\ x_(rms)=1.85*10^{-3\text{ }}m \end{gathered}`

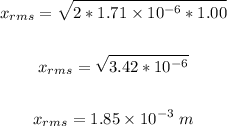
Therefore, the average distance a perfume molecule moves in one second in air is 1.85 x 10⁻³ m

ANSWER:

1.85 x 10⁻³ m