In order to find the magnitude of the vector sum, proceed as follow:
Calculate the vertical and horizontal components of A, as follow:
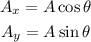
where,
A: magnitude of A vector = 4.00N
θ: direction related to B = 60.0 degrees
Replace the previous values into the expressions for Ax and Ay and simplify:
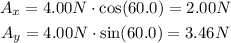
Now, consider that B vector can have only a horizontal component, then, its magnitude is just the value of Bx (it is possible because there is no specifications about the orientation of the vectors in the coordinate system):
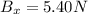
Next, consider that the sum vector S has the following components:
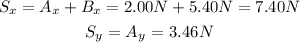
And the magnitude of the sum vector S is:
![S=\sqrt[]{S^2_x+S^2_y}=\sqrt[]{(7.40N)^2+(3.46N)^2}\approx8.17N](https://img.qammunity.org/2023/formulas/physics/college/pydrworczfxdoslalmol3y3bxc52d8jiqt.png)
Hence, the magnitude of the vector sum is approximately 8.17N