If y varies directly with x, with a constant of proportionality k, then the equation that relates x and y is:
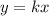
To solve the problem, use the first pair of data x=4, y=-16 to find the value of the constant of proportionality k. Next, use the value of k to write down the equation that relates x and y for this case, and use it to find the value of y when x=9.
Replace y=-16 and x=4 into the equation and solve for k:
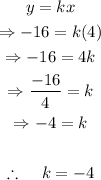
Since the value of k is -4, then the equation that relates x and y is:
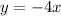
Replace x=9 to find the value of y when x=9.

Therefore, the answers are:
Equation: y=-4x
Solution: y=-36