Question

Determine whether there is a minimum or maximum value to the quadratic function.h(t) = −8t2 + 2t − 1Find the minimum or maximum value of h.Find the axis of symmetry.

Answer 1

For a quadratic function in the form:

`f(x)=ax^2+bx+c`

If a>0 the function opens up, it has a minimum

If a<0 the function opens down, it has a maximum

Axis of symmetry is x= -b/2a

Vertex: (-b/2a, f(-b/2a)), f(-b/2a) is the maximum or minimum value

For the given function:

`h(t)=-8t^2+2t-1`

a= -8

Parabola opens down. It has a maximum value

Find the axis of symmetry:

`t=-(2)/(2(-8))=(-2)/(-16)=(1)/(8)`

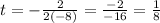
Find the y-coordinate of the vertex:

`\begin{gathered} h((1)/(8))=-8((1)/(8))\placeholder{⬚}^2+2((1)/(8))-1 \\ \\ h((1)/(8))=-8((1)/(64))+(2)/(8)-1 \\ \\ h((1)/(8))=-(1)/(8)+(2)/(8)-1 \\ \\ h((1)/(8))=(1)/(8)-1 \\ \\ h((1)/(8))=(1-8)/(8) \\ \\ h((1)/(8))=-(7)/(8) \end{gathered}`

______________

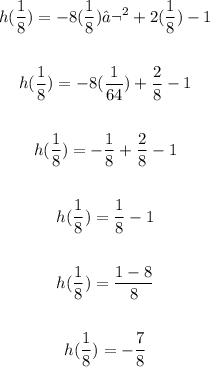
Then, the given function has a maximum value, the maximum value is -7/8, and the axis of symmetry is t=1/8