Question

A golf ball is hit and lands 53 m away. The path of the ball took it just over a 9 m tree. Determine a function that models the path of the golf ball.

Answer 1

Given that a golf ball is hit and lands 53 m away and that the path of the ball took it just over a 9 m tree. We can determine a function that models the path of the golf ball below

Step-by-step explanation

If the ball covers a distance of 53 and attains a height of 9 meters, we can draw the diagram below

From the above, if we let x be the starting point of the golf balll, the landing point becomes

x+53.

We can then model the equation to give;

`\begin{gathered} y=a(x)(x+53) \\ y=ax^2+53ax \\ y^(\prime)=2ax+53a=0 \\ 2ax=53a \\ x=(53a)/(2a) \\ x=26.5 \end{gathered}`

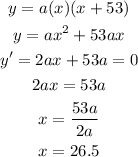
Therefore, at maximum height when x=26.5, y =9