To determine the distinguishable permutations of the given word, here are the steps.
1. Count the number of letters in the given word. In the word EFFECTIVE, there are 9 letters.
2. Calculate 9!.
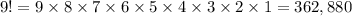
3. Determine what are the letters found in the word effective and count how many times the letter occurred.
Letter E - 3 times
Letter F - 2 times
Letter C - 1 time
Letter T - 1 time
Letter I - 1 time
Letter V - 1 time
4. Get the product of the factorial of the letters that occurred more than once.
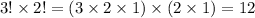
5. Divide the result of step 2 by the result of step 4.
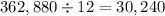
Therefore, there are 30,240 different permutations of the word EFFECTIVE.