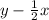The blue region consists on the intersection of two regions. The region above the decreasing line, and the region below the increasing line. Those lines are
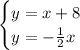
Those are the boundaries of those regions. Since both lines are dashed lines, the regions do not include those lines. The increasing line is the one with the positive slope

Since our region is below this line, the y values must be less than the values on this line, and the inequality that represents this region is
![yThe decreasing line is the one with the negative slope[tex]y=-(1)/(2)x](https://img.qammunity.org/2023/formulas/mathematics/college/dy4dtgstk5akupmd3gbgv42mkb7qh38wh1.png)
Since our region is above this line, the y values must be greater than the values on this line, and the inequality that represents this region is

Combining those two regions, we have their intersection which is the desired blue region