Step 1
see the figure below to better understand the problem
Step 2
Applying the law of sines
Find out the area of triangle ABC
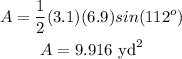
Step 3
Applying the law of cosines
Find out the length of the side AC
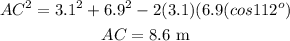
Step 4
Applying the law of cosines
Find out the measure of angle D
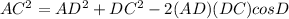
substitute given values
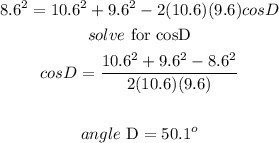
Step 5
Applying the law of sines
Find out the area of the triangle ADC
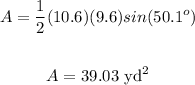
The area of the quadrilateral is equal to
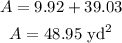
The area is 48.95 square yards (rounded to two decimal places)