The function we have is:
Let's find the derivative using the product rule and the quotient rule.
-Using the product rule.
This is the better method for finding the derivative of this function because the function is already a product between two functions, which we will call f(alpha) and g(alpha):
The product rule we will use is as follows:
Where the ' means derivative.
Let's first calculate the derivative of function f and g:
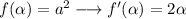
here we have used the following rule of derivation:
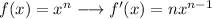
Now we find the derivative of g:
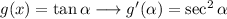
This is a derivate that we can find tables of derivation.
Now, we apply the product rule mentioned earlier:
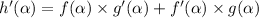
And substitute all of the known values:
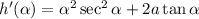
That is our final result.
We can also calculate this using the quotient rule.
As we mentioned at the beginning, since there is a multiplication it is better to use the product rule to find the derivative, but we can also find it by using the quotient rule.
To use the quotient rule there need to be a division in the function, so we modify the original function:
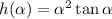
And express it as a division as follows:
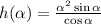
This is because
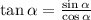
To use the quotient rule, we need to take or function:
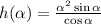
And define one function f to be the numerator, and another function g to be the denominator:

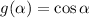
And the quotient rule is:

Before we find this, we need the derivatives of g and f:
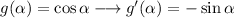
And for the derivative of f we apply the product rule because there is a multiplication:
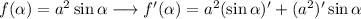
Solving the derivatives of this product rule:
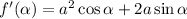
And now we are ready to use the quotient rule:

Substituting the known values:
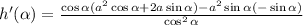
Simplifying the expression:
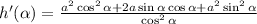
We factor the terms that contain a^2:

Here, we use the following property of the cosine and the sine:
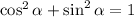
And we simplify again:
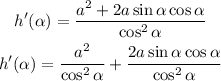
We simplify further using:
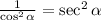
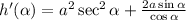
which is equal to:
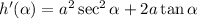
Answer: