As the rick is thrown straight up in the air and the function of its displacement is quadratic it means that the rock traveled a distance up to its maximum and then down to the ground. Then, the function value in the maximum is half the distance traveled by the rock.
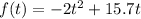
Use the next formula to find the time (t) in the maximum point of quadratic function:
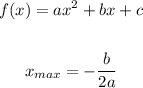
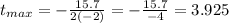
Evaluate the function for t=3.925 to find the maximum value:
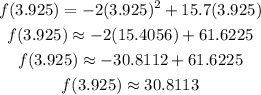
Multiply the maximum value by 2 to get the total distance traveled by the rock:
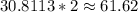
Then, the total distance traveled by the rock when it reaches the ground is 61.62metersAnswer: C