-×^2 - 7x + 7 = -2x^2 to the nearest tenth.

Question

asked Jul 3, 2023 228k views

1 Answer

Jxstanford · Answer 1 · 2023-07-06T14:02:48+0000

Solving Quadratic Equations

The general form of a quadratic equation is:

It can be solved by using the formula:

$x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}$

we have the following equation:

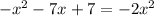
we need to put this equation in standard form as explained above

Adding 2x^2:

$\begin{gathered} 2x^2-x^2-7x+7=-2x^2+2x^2 \\ \text{Simplifying:} \\ x^2-7x+7=0 \end{gathered}$

Now we have the equation in the correct form, we find the value of the variables as follows:

a=1, b=-7, c=7

Applying the formula:

$x=\frac{-(-7)\pm\sqrt[]{(-7)^2-4(1)(7)}}{2(1)}$

Operating:

$x=\frac{7\pm\sqrt[]{49-28}}{2}=\frac{7\pm\sqrt[]{21}}{2}$

The square root of 21 is not exact, we use two decimals so far, and we'll round to one decimal at the very last time.

Taking the square root:

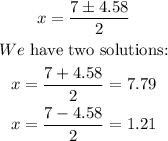
$\begin{gathered} x=(7\pm4.58)/(2) \\ We\text{ have two solutions:} \\ x=(7+4.58)/(2)=7.79 \\ x=(7-4.58)/(2)=1.21 \end{gathered}$

The solutions (to the nearest tenth) are:

x= 7.8

x=1.2

Answer complete

Did you understand the explanation?

You are very welcome!

Feel free to let me know how I did by rating our session once you close it