Question

1. Rationalize the numerator of the expression below and simplify your answer.V3 - 2V12+1A

Answer 1

`(-1)/(8+5√(3))`

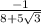
The expression we have is:

`(√(3)-2)/(√(12)+1)`

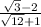
To rationalize the numerator we must do as follows:

`(√(3)-2)/(√(12)+1)\cdot(√(3)+2)/(√(3)+2)`

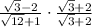
We multiply the whole expression by the numerator, but we change the sign.

Next, we combine the two fractions:

`((√(3)-2)(√(3)+2))/((√(12)+1)(√(3)+2))`

Now we use the distributive property to multiply each term (this is to multiply each term in each parenthesis by each term in the other parenthesis besides them).

`(√(3)\cdot√(3)+2√(3)-2√(3)-2\cdot2)/(√(12)\cdot√(3)+2√(12)+1\cdot√(3)+1\cdot2)`

We simplify the multiplications, and cancel the two middle terms in the numerator:

`\begin{gathered} (√(3\cdot3)-4)/(√(12\cdot3)+2√(12)+√(3)+2) \\ \end{gathered}`

we simplify again:

`(√(9)-4)/(√(36)+2√(12)+√(3)+2)`

We solve the square roots of 9 (which is 3) and 36 (which is 6)

`(3-4)/(6+2√(12)+√(3)+2)`

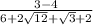
Solving the numerator

`(-1)/(6+2√(12)+√(3)+2)`

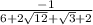
And finally what we can do simplify further is to express the square root of 12 as follows:

`√(12)=√(4\cdot3)=2√(3)`

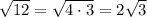
Substituting this into our expression:

`\begin{gathered} (-1)/(6+2(2√(3))+√(3)+2) \\ \\ (-1)/(6+4√(3)+√(3)+2) \end{gathered}`

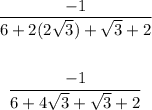
We add 4 and 1 square roots of 3 in the denominar and get 5 square root of 3:

`(-1)/(8+5√(3))`

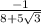
also we added 6+2 which is 8.

That is the simplified answer.