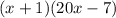Question

Completely factor the trinomial, if possible. 20x^2+13x-7

Answer 1

The trinomial is given to be:

`20x^2+13x-7`

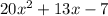
STEP 1:

Rewrite the middle term such that we can break the expression. Multiply the first and last terms of the expression:

`20x^2*(-7)=-140x^2`

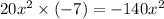
Find two multipliers of -140x² that will add up to +13x:

`Multipliers=20x,-7x`

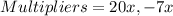
Replace 13x in the expression by the multipliers:

`20x^2+20x-7x-7`

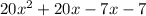
STEP 2:

Collect the common terms in each pair of numbers:

`\Rightarrow20x(x+1)-7(x+1)`

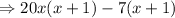
STEP 3:

Factor the expression by collecting the like terms:

`\Rightarrow(x+1)(20x-7)`

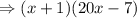
ANSWER:

The factored expression is:

`(x+1)(20x-7)`