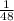SOLUTION
The man has 4 pairs of shoes
3 suits and
4 shirts
Probability is given as
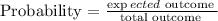
If he is to pick his favorite pair of shoes, suit and shirts, it means he will pick 1 pair of shoe, 1 suit and 1 shirt.
Then the probability of picking
His favorite pair of shoes becomes
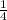
Then the probability of picking
His favorite suit becomes

And Then the probability of picking
His favorite shirt becomes
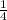
Hence the required probability is
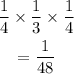
Hence the answer is