Given the system of equations:
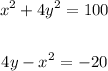
Let's find the sum of the x-coordinates of all solutions.
Let's solve the system simultaneously using substitution method to find the solution.
• Rewrite the second equation for x²:

• Substitute 4y + 20 for x² in the first equation:
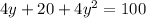
Now, let's find the values of y
Subtract 20 from both sides

Set each factor to zero and solve for y:

We have the solutions for y:
y = 4 and -5
Now, let's find the values of x when y = 4 and -5
• When y = 4:
Substitute 4 for y in either of the equations and solve for x.
Take equation 1:
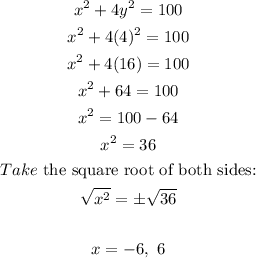
• When y = -5:
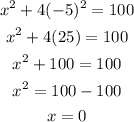
Therefore, the values of x are:
-6, 6, 0
The sum of the x-coordinates is:
-6 + 6 + 0 = 0
ANSWER:
0