Given -
A cone and a cylinder have equal radii = r,
and equal altitudes = h
The slant height of the cone = l
To Find -
The ratio of the lateral area of the cone to the lateral area of the cylinder =?
Step-by-Step Explanation -
The lateral surface area of the cylinder = 2πrh
The lateral surface area of the cone = πrl
So,
The ratio of the lateral area of the cone to the lateral area of the cylinder =
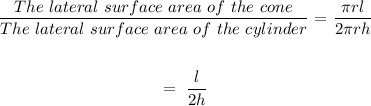
Final Answer -
The ratio of the lateral area of the cone to the lateral area of the cylinder =
A. l:2h