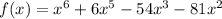Question

Find a polynomial function of degree 6 with a leading coefficient of 1 and with - 3 as a zero of multiplicity 3, 0 as a zero of multiplicity 2, and 3 as a zero of multiplicity 1

Answer 1

Given, that a polynomial has the following:

The degree = 6

The leading coefficient = 1

The zeros are as follows:

-3 as a zero of multiplicity 3 ⇒ The corresponding factor = (x+3)

0 as a zero of multiplicity 2 ⇒ The corresponding factor = x

3 as a zero of multiplicity 1 ⇒ The corresponding factor = (x-3)

So, the equation of the polynomial written in factor form will be as follows:

`f(x)=x^2(x-3)(x+3)^3`

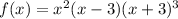
Expand the polynomial:

`\begin{gathered} f(x)=x^2(x-3)(x^3+9x^2+27x+27) \\ f(x)=(x^3-3x^2)(x^3+9x^2+27x+27) \\ f(x)=x^3(x^3+9x^2+27x+27)-3x^2(x^3+9x^2+27x+27) \\ f(x)=x^6+9x^5+27x^4+27x^3-3x^5-27x^4-81x^3-81x^2 \end{gathered}`

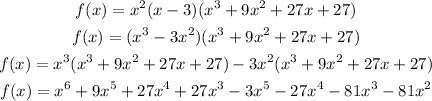
Combine the like terms:

So, the answer will be:

`f(x)=x^6+6x^5-54x^3-81x^2`