Question

Find the lengths of diagnosis AC and BD for the parallelogram where EB = x + 17, ED = 3y + 2, EA= 8x + 1 and EC = 6y - 11. SHOW ALL WORK.

Answer 1

Given:

EB = x + 17

ED = 3y + 2

EA = 8x + 1

EC = 6y - 11

Let's find the lengths of digonals AC and EB.

To find the lengths of the lengths of the diagonals, we have the set of equations:

8x + 1 = 6y - 11

x + 17 = 3y + 2

Let's solve the equations simultaneously using substitution method.

8x + 1 = 6y - 11...........................equation 1

x + 17 = 3y + 2.............................equation 2

From equation 2, write the equation for x:

Subtract 17 from both sides in equation 2:

x + 17 - 17 = 3y + 2 - 17

x = 3y -15..................equation 3

Substitute (3y - 15) for x in equation 1:

8(3y - 15) + 1 = 6y - 11

Apply distributive property:

8(3y) - 8(15) + 1 = 6y - 11

24y - 120 + 1 = 6y - 11

24y - 119 = 6y - 11

Add 119 to both sides:

24y - 119 + 119 = 6y - 11 + 119

24y = 6y+108

Subtract 6y frm both sides:

24y - 6y = 6y - 6y + 108

18y = 108

Divide both sides by 18:

`\begin{gathered} (18y)/(18)=(108)/(18) \\ \\ y=6 \end{gathered}`

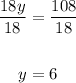
Substitute 6 for y in equation 3:

x = 3y - 15

x = 3(6) - 15

x = 18 - 15

x = 3

We have the values of x and y:

x = 3, y = 6

Let's find the length of the diagonals:

Length of AC:

AC = EA + EC

AC = 8x + 1 + 6y - 11

Substitute 3 for x and 6 for y

AC = 8(3) + 1 + 6(6) - 11

AC = 24 + 1 + 36 - 11

AC = 50

Length of BD:

BD = EB + ED

BD = x + 17 + 3y + 2

Substitute 3 for x and 6 for y:

BD = 3 + 17 + 3(6) + 2

BD = 3 + 17 + 18 + 2

BD = 40

Therefore, the lengths of the diagonals are:

AC = 50

BD = 40

ANSWER:

AC = 50

BD = 40