The volume of a triangular pyramid is given by
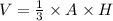
where H is the heigh of the pyramid and A is the base of the triangular base. In our case,
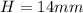
and the base area is
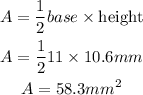
where
Then, by substituting our last result into the volume formula, we have
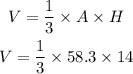
which gives
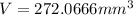
Therefore, by rounding to the nearest thousandth, the answer is: 272.067 cubic milimeters