Let's draw a picture of our problem:
where h is the height of the ballon. Since we have a right triangle, we can use a trigonometric function to relate the height, the distance from the observer to the ballon and the given angle. This function is the sine function, that is
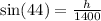
so, by moving 1400 to the left hand side, we get
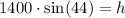
then, h is given by

Now, lets find the position directly beneath the balloon. This is given by d in our picture. Then, we must relate d with the given angle and 1400 m. This function is the cosine function of 44 degrees. that is,
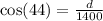
hence, by moving 1400 to the left hand side, we have
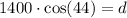
so, d is given by
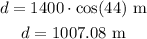
Therefore, the answers are:
How high is the balloon? 972.52 meters
How far is it to a position directly beneath the balloon? 1007.08 meters