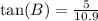Question

11 1 point Find the trig ratio for tan(B)? 5 1 B 2 O 3 4 10.9

Answer 1

Notice that the triangle △ABC is a right triangle. The side AB is the hypotenuse of the triangle, since it is opposed to the right angle C.

The tangent of the angle B is given by the ratio of the lengths of the side opposite to it and the side adjacent to it. Then:

`\tan (B)=(AC)/(BC)`

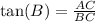
From the Pythagorean Theorem, we know that:

`AC^2+BC^2=AB^2`

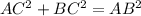
Substitute the values AC=5 and AB=12 and solve for BC:

`\begin{gathered} 5^2+BC^2=12^2 \\ \Rightarrow BC^2=12^2-5^2 \\ \Rightarrow BC^2=144-25 \\ \Rightarrow BC^2=119 \\ \Rightarrow BC=\sqrt[]{119} \end{gathered}`

Once we know the value of BC, substitute the lengths of AC and BC to find the tangent of B:

`\tan (B)=\frac{5}{\sqrt[]{119}}`

Since the square root of 119 is approximately 10.9, then:

`\tan (B)=(5)/(10.9)`