Question

Consider the function.4x - 59 (x) =(0,5)x² – 1'(a) Find the value of the derivative of the function at the given point.g'(0) =(b) Choose which differentiation rule(s) you used to find the derivative. (Select all that apply.)power rulequotient ruleproduct rule

Answer 1

In order to find the derivative for the division of two functions we need to apply the quotient rule,

`\begin{gathered} (f(x))/(g(x)) \\ (d)/(dx)\lbrack(f(x))/(g(x))\rbrack=(g(x)f^(\prime)(x)-f(x)g^(\prime)(x))/((g(x))^2) \end{gathered}`

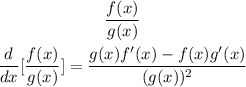
then, using the power rule of differentiation find the derivative of both numerator and denominator

`\begin{gathered} (4x-5)/(x^2-1) \\ derivative\text{ for the numerator: 4} \\ derivative\text{ for the denominator: 2x} \end{gathered}`

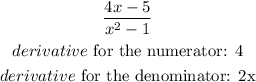
apply the quotient rule

`\begin{gathered} g^(\prime)(x)=((x^2-1)(4)-(4x-5)2x)/((x^2-1)^2) \\ g^(\prime)(x)=(4x^2-4-8x^2+10x)/((x^2-1)^2) \\ g^(\prime)(x)=(-4x^2+10x-4)/((x^2-1)^2) \end{gathered}`

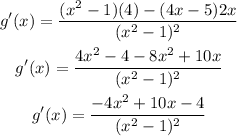
evaluate the derivative on 0,

`\begin{gathered} g^(\prime)(0)=(-4(0)^2+10(0)-4)/((0^2-1)^2) \\ simplify, \\ g^(\prime)(0)=(-4)/((-1)^2) \\ g^(\prime)(0)=-4 \end{gathered}`

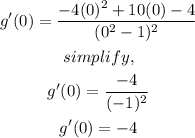
Answer:

a) g'(0)= -4

b) quotient rule and power rule