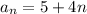Given:
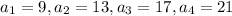
To find:
The nth term formula.
Step-by-step explanation:
The nth term formula is,
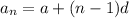
The first term a = 9.
The common difference is,
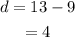
So, the nth term formula for the sequence is,
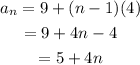
Therefore, the nth term formula is,
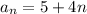
Final answer:
The nth term formula is,