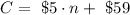Question

The total cost, c, of renting a canoe for n hours can be represented by a system of equations. a. Write the system of equations that could be used to find the total cost, c, of renting a canoe for n hours.b. Graph the system of equations.c. When would the total cost for renting a canoe in be the same on both rivers?

Answer 1

From the given infomation, the cost for river Y is constant, that is,

`\begin{gathered} Y=\text{ \$33+\$13} \\ Y=\text{ \$46} \end{gathered}`

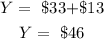
where Y denotes the cost for river Y.

On the other hand, the cost for river Z is given by

`Z=\text{ \$5}\cdot n+\text{ \$13}`

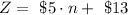
where n denotes the number of hours and Z the cost for river Z.

Therefore, the Total cost (C) will be the sum of the cost for river Y and river Z, that is,

`C=\text{ \$46+\$5}\cdot n+\text{ \$13}`

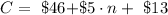
which gives

`C=\text{ \$5}\cdot n+\text{ \$}59`