Step 1: Compute the rate in meters per seconds
![\begin{gathered} 1\operatorname{km}\text{ }=1000m \\ 1h=60*60s \end{gathered}]()
Therefore,
![\begin{gathered} 198\operatorname{km}\text{ / h }=\frac{198\operatorname{km}}{1h} \\ \text{Thus,} \\ 198\operatorname{km}\text{ / h }=(198*1000m)/(60*60s) \\ 198\operatorname{km}\text{ / h }=(198*10m)/(6*6s) \\ 198\operatorname{km}\text{ / h }=(33*10m)/(1*6s) \end{gathered}]()
Hence,
![198\operatorname{km}\text{ / h }=(11*10m)/(1*2s)=55m\text{ /s}]()
Therefore, the rate in meters per seconds is 55 m/s
Step 2: Compute the number of metes the parachutist will fall in 2s at this rate (55m/s)
At the rate of 55m/s, the distance the parachutist falls in 2s is given by
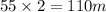
Hence, the number of meters is 110m