Question

One positive integer is 1 less than twice another. The sum of their squares is 34. Find the integers.

Answer 1

Let's define the following variable.

x = first integer

y = second integer

If the sum of their squares is 34, then we can form the equation below:

`x^2+y^2=34`

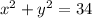
If the other integer, say x, is 1 less than twice the other (y), then we can form this second equation:

`x=2y-1`

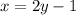
From these two equations, we can now solve for the values of x and y.

Here are the steps.

1. Replace the value of "x" in equation 1 using the value in equation 2.

`(2y-1)^2+y^2=34`

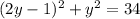
2. Apply the exponent.

`\begin{gathered} (4y^2-4y+1)+y^2=34 \\ 4y^2-4y+1+y^2=34 \end{gathered}`

3. Rearrange the terms. Subtract 34 on both sides of the equation then, combine similar terms.

`\begin{gathered} 4y^2+y^2-4y+1=34 \\ 4y^2+y^2-4y+1-34=34-34 \\ 5y^2-4y-33=0 \end{gathered}`

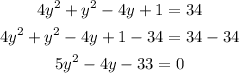
In step3, we are able to create a quadratic equation in a standard form that is ax² + bx + c wherein a = 5, b = -4, and c = -33.

To solve for the value of y, we can use the Quadratic formula.

`y=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Since we have already determined the values of a, b, and c, let's plug them into the formula above.

`y=\frac{-(-4)\pm\sqrt[]{(-4)^2-4(5)(-33)}_{}}{2(5)}`

Then, solve for y.

`\begin{gathered} y=\frac{4\pm\sqrt[]{16+660}}{10} \\ y=\frac{4\pm\sqrt[]{676}}{10} \\ y=(4\pm26)/(10) \end{gathered}`

Separate the plus and minus signs.

`\begin{gathered} y=(4+26)/(10)=(30)/(10)=3 \\ y=(4-26)/(10)=-(22)/(10)=-2.2 \end{gathered}`

There are two possible values y but only one is an integer. So, we will use y = 3.

To solve for the other integer x, let's use the second equation plugin y = 3.

`\begin{gathered} x=2y-1 \\ x=2(3)-1 \\ x=6-1 \\ x=5 \end{gathered}`

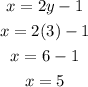
Therefore, the integers are 5 and 3.