Answer:
After 6 months, Casey would have paid $330 at either gym.
Step-by-step explanation:
Let the number of months be represented by the variable t.
One gym has a $120 joining fee and costs $35 per month.
The equation representing the amount paid for this gym is:
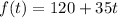
Another gym has no joining fee and costs $55 per month.
The equation representing the amount paid for this gym is:
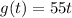
When the amount to be a member is the same, we have that:

We solve for t.
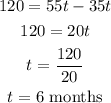
The amount that would have been paid will be:
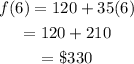
After 6 months, Casey would have paid $330 at either gym.