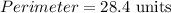The coordinates of the parallelogram are given to be:
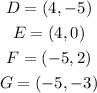
The graph is shown below:
To get the perimeter of the shape, the lengths of the lines are to be calculated.
According to the property of a parallelogram, the opposite sides are equal. Therefore:
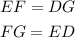
The length of line ED can be calculated to be:
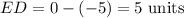
The length of line EF can be calculated using the distance formula:
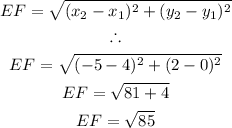
Therefore, the perimeter is calculated as follows:
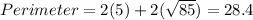
ANSWER